算法差分约束

差分约束算法的提出巧妙地将数学上的方程和不等式与图论相结合，让我们能够很好地处理与不等式相关的整数问题。

理论推导

差分约束系统

一个由 \(n\) 个变量 \(x_1, x_2, \cdots , x_n\) （一般为整型）和 \(m\) 个形如 \((a_i, b_i, k_i)\) , 使 \(x_{a_i} - x_{b_i} \leqslant (\geqslant) k_i\) 的约束条件组成的不等式组称为差分约束系统。利用差分约束算法，我们可以很方便地求得差分约束系统的一组解。下例便是一个典型的差分约束系统。

\[\left\{ \begin{aligned} x_{a_1} - x_{b_1} &\leqslant k_1 \\ x_{a_2} - x_{b_2} &\leqslant k_2 \\ &\vdots \\ x_{a_m} - x_{b_m} &\leqslant k_m \\ \end{aligned}\right.\]

从最短路到不等式组

这样的一个差分约束系统，其中的每一个约束，可以注意到其形式与图论中求最短路的松弛过程中用到的三角不等式形式相类似。

以下以小于等于形式的约束条件为例。对比约束条件与最短路算法中的松弛操作：

\[x_{a_i} - x_{b_i} \leqslant k_i\]

\[dis_v - dis_u \leqslant w_{u, v}\]

其中下式便是由最短路算法中的 \(dis_v \leqslant dis_u + w_{u, v}\) 一式变形而来。

上面两式对照，便引出了变量与点、约束条件与边的对应关系。对于每一组约束 \((a_i, b_i, k_i)\) ，连接一条边 \(G_i: (b_i \to a_i, k_i)\) 建图，之后再在建成的图上求得一组合法的最短路径 \(dis\) , 那么对应每一个变量 \(x_i\) , \(dis_i\) 就是其对应的解。

举例来看，对于以下 \(n = 3, m = 3\) 的一组差分约束系统，我们只需要依照对应法则建好三条边，然后在得到的图上求一遍最短路即可。

\[\left\{ \begin{aligned} x_2 - x_1 &\leqslant 3 \\ x_3 - x_2 &\leqslant -2 \\ x_3 - x_1 &\leqslant 1 \\ \end{aligned}\right.\]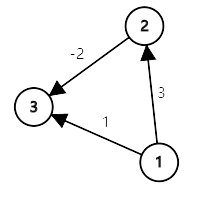

对于上图，一组合法的最短路径便是 \(dis_1 = 0, dis_2 = 3, dis_3 = 1\) ，这就是原约束条件下的一组合法解。

而再考虑到若是原图中存在负环，那么 \(dis\) 无解，对应的就是原方程无解。在此不给出严谨证明，只是通过一组例子理解其合理性。

稍微修改一下上面的例子，得到

\[\left\{ \begin{aligned} x_2 - x_1 &\leqslant 3 \\ x_3 - x_2 &\leqslant -2 \\ x_1 - x_3 &\leqslant -2 \\ \end{aligned}\right.\]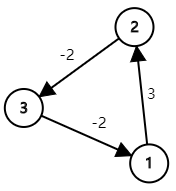

此时，将三个不等式相加后，不等式转变为 \(0 \leqslant -1\) , 显然可见原不等式组无解。而正是这三个约束条件在图中构成了一个负环。

故存在结论：在按照最短路方式构建的图中，只要找出一组可行的最短路解，便能够找出原不等式组的一组解。若图中存在负环，则不等式组无解。

从最长路的角度建图

注意到差分约束系统中的符号不仅可以是小于等于，也可以是大于等于。再遇到这类大于等于条件时，诚然可以通过变形来转化为之前的小于等于的形式来求解，也可以通过求最长路来求解。

与最短路类似，最长路的“松弛”操作也与大于等于的条件类似，此处不再打出。

这里通过一组样例阐述如何用最长路求解。例子与之前的第一个例子相同，但是将其变形为大于等于的形式。注意，建边方向仍然是由减数指向被减数。

\[\left\{ \begin{aligned} x_1 - x_2 &\geqslant -3 \\ x_2 - x_3 &\geqslant 2 \\ x_1 - x_3 &\geqslant -1 \\ \end{aligned}\right.\]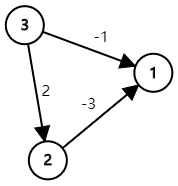

可以看出， \(dis_1 = 0, dis_2 = 3, dis_3 = 1\) 仍然是合法的一组最长路，其依然能够得出一组正确的解。同时因为求最长路，所以若图中存在正环则无解。

故存在结论：在按照最长路方式构建的图中，只要找出一组可行的最长路解，便能够找出原不等式组的一组解。若图中存在正环，则不等式组无解。

求最短路和最长路的方法

以下内容均以最短路建图为例，最长路方法可以类比得出。

一般而言，采取方法都是直接设置一超级源点，假设其下标为 0 ，并从其向每一个点连出一条长度为 0 的边，以简单求得一个合法的解。若是从数学意义上思考，便是设置一个变量 \(x_0\) , 并使得

\[\left\{ \begin{aligned} &x_0 = 0 \\ &x_i - x_0 \leqslant 0 \quad (i = 1, 2, \cdots , n) \\ \end{aligned}\right.\]

然后从 0 号点开始，跑一遍单源最短路经即可。

最长路与最短路的区别

以下按照最短路方式建的图称为最短路图，最长路图亦然。可以看出，实际上最长路图就是最短路图的边全部反向，边权全部取负，其本质是相同的。

不过从其数学意义上讲，存在一个结论：若是以最短路建图，那么跑一个点的单源最短路径，得出的每个点解是其理论上的最大解；而若是以最长路建图，跑一个点的单元最长路径，得出的每个点的解是其理论上的最小解。

这个结论也很好理解，因为最短路的松弛操作便是将一个点的解的上限不断按照条件减小，最终得出来的答案便是理论上的最大解；最长路的“松弛”操作与其相反。这个最长路与最短路的性质在我们解决一些问题时会提供很大的帮助。利用此性质，我们在想求最大解时，便可以建最长路图；在求最小解时，便建最短路图。

总结出的一些建图经验

注意题目中给出的隐性条件，比如序列 \(x_i\) 相邻量之间的关系；
\(x_a - x_b = c\) 可以拆分成 \(x_a - x_b \leqslant c\) 和 \(x_a - x_b \geqslant c\) ， \(x_a - x_b > c\) 在整数意义下可以改成 \(x_a - x_b \geqslant c +1\) ；
判断负环时若有超级源点，那么入队次数大于 n 时才能判断有负环；
必要时可以考虑利用前缀和构造序列，寻找差分约束条件；
充分利用最短路图和最长路图的性质，灵活选取起始点，有时可以不用超级源点；
有时考虑全局情况下可以用 floyd 求全局最短（长）路解题。
有时可以同时建立最短路图和最长路图，分别跑最短（长）路，求得未知数的取值范围；
有时出题人数据毒瘤，可以考虑 SPFA 的优化。本文涉及 swap-SLF 优化。
有时出题人数据毒瘤，可以考虑时间判负环，但是有一定的错误率。

代码实现

最短路、判断负环

由于存在负权边，Dijkstra 不可用。Floyd 过于简单，在此省略，并给出 SPFA 的一种优化的实现方式。当然，平时的非毒瘤题用裸 SPFA 即可。

带 swap-SLF 优化的 bfs-SPFA: 每次改变队列后，若队首距离大于队尾，则交换首尾。可以避免被一些毒瘤数据卡。

const int INF = 0x7f7f7f7f;
int dis[NMAX];

bool SPFA(int begin)
{
    bool inq[NMAX];
    int vis[NMAX];
    deque<int> que;
    memset(dis, INF, sizeof(dis));
    memset(inq, 0, sizeof(inq));
    memset(vis, 0, sizeof(vis));

    dis[begin] = 0;
    que.push_back(begin), inq[begin] = true, vis[begin]++;
    while (!que.empty())
    {
        int fnt = que.front();
        que.pop_front(), inq[fnt] = false;
        if (dis[que.front()] > dis[que.back()]) // swap-SLF
            swap(que.front(), que.back());
        for (register edge *i = head[fnt]; i; i = i->nxt)
            if (dis[i->to] > dis[fnt] + i->w)
            {
                dis[i->to] = dis[fnt] + i->w;
                if (!inq[i->to])
                {
                    que.push_back(i->to), inq[i->to] = true, vis[i->to]++;
                    if (dis[que.front()] > dis[que.back()]) // swap-SLF
                        swap(que.front(), que.back());
                    if (vis[i->to] >= n)
                        return false;
                }
            }
    }
    return true;
}

最长路，判断正环

至于最长路的求解，只能用 SPFA 或 Floyd ，Dijkstra 由于其贪心本质无法求解最长路。SPFA 和 Floyd 求解最长路代码与最短路基本相同，只有两点修改：

对于 SPFA 中的 dis 数组，初始化为负无穷。在此有一技巧，可以定义 NINF = 0x80808080 ，以适用于 memset() 函数。
对于二算法的松弛操作，将‘>’改为‘<’即可。

更加详细地，在此给出 SPFA 算法求最长路的代码片段。

const int NINF = 0x80808080; // 负无穷
int dis[NMAX];

bool SPFA(int begin)
{
    bool inq[NMAX];
    int vis[NMAX];
    queue<int> que;
    memset(dis, NINF, sizeof(dis));
    memset(inq, 0, sizeof(inq));
    memset(vis, 0, sizeof(vis));

    dis[begin] = 0;
    que.push(begin), inq[begin] = true, vis[begin]++;
    while (!que.empty())
    {
        int fnt = que.front();
        que.pop(), inq[fnt] = false;
        for (register edge *i = head[fnt]; i; i = i->nxt)
            if (dis[i->to] < dis[fnt] + i->w) // 松弛条件
            {
                dis[i->to] = dis[fnt] + i->w;
                if (!inq[i->to])
                {
                    que.push(i->to), inq[i->to] = true, vis[i->to]++;
                    if (vis[i->to] >= n)
                        return false;
                }
            }
    }
    return true;
}

模板与例题

P5960 【模板】差分约束算法 - 洛谷计算机科学教育新生态
 题解洛谷P5960 【模板】差分约束算法 | 散虑の春雨寻风

P2294 [HNOI2005]狡猾的商人 - 洛谷计算机科学教育新生态
难度较低，转化后直接判断有无解即可。

SP116 INTERVAL - Intervals - 洛谷计算机科学教育新生态
 1508 Instervals - ZOJ
需要转化并求最小解，考虑最长路。

P3275 [SCOI2011]糖果 - 洛谷计算机科学教育新生态
重点在于对不同等式条件的转化。

P3530 [POI2012]FES-Festival - 洛谷计算机科学教育新生态
 题解 [POI2012] FES-Festival | 散虑の春雨寻风
较为综合，需要全局考虑约束条件并结合其他算法。

P3084 [USACO13OPEN]Photo G - 洛谷计算机科学教育新生态
 题解 [USACO13OPEN]Photo G | 散虑の春雨寻风
正解为动态规划，但是差分约束在经过优化处理后也可通过。

P2474 [SCOI2008]天平 - 洛谷计算机科学教育新生态
思维难度较大，重点在差分约束条件的寻找，考虑建多个图以求取值范围。

1420 Cashier Employment - ZOJ
1275 -- Cashier Employment - POJ
U133833 店主的困惑 (Puzzlement of Merchant) – 洛谷计算机科学教育新生态
 题解 POJ1275 Cashier Employment | 散虑の春雨寻风
建议使用 POJ 或洛谷平台，数据较为全面。

参考资料

冯威《数与图的完美结合——浅析差分约束系统》

2020-08-06 Update: 增加了最长路和判断正环的代码，修正部分笔误。
2020-08-07 Update: 修正部分笔误（理论推导-从最短路到不等式组）
2020-10-07 Update: 添加题目 Cashier Employment 的 OJ 源和题解。
2021-03-07 Update: 修复图像显示错误。