例题
2021全国I卷
已知函数 \(f(x) = x(1 - \ln x)\).
(1)讨论 \(f(x)\) 的单调性.
(2)设 \(a, b\) 为两个不相等的正数,且 \(b \ln a - a\ln b = a - b\),证明:\(2 < \dfrac{1}{a} + \dfrac{1}{b} < e\).
第一问:函数单调性
由于难度较低,此处省略部分过程。
\(f(x)=x-x\ln x\)
\(f'(x)=-\ln x\)
| \(x\) | \((0,1)\) | 1 | \((1,+\infty)\) |
|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(f(x)\) | \(\nearrow\) | 大 | \(\searrow\) |
第二问:极值点偏移
观察条件式子较为对称,尝试变量分离。
\(\Rightarrow\) \(\dfrac{\ln a}{a} - \dfrac{\ln b}{b} = \dfrac{1}{b} - \dfrac{1}{a}\)
\(\Rightarrow\) \(\dfrac{1}{a} - \dfrac{\ln \frac{1}{a}}{a} = \dfrac{1}{b} - \dfrac{\ln \frac{1}{b}}{a}\)
令 \(x_a = \dfrac{1}{a}\),\(x_2 = \dfrac{1}{b}\),则有 \(f(x_1) = f(x_2)\).
只要证 \(2 < x_1 + x_2 < e\) 即可.
法一:对称
先证 \(x_1+x_2>2\).
从几何角度考虑,此方法相当于将函数 \(f(x)\) 沿着 \(x=1\) 作对称,故称之为对称法。
构造函数 \(g(x)=f(1+x) - f(1-x)\) 或 \(g(x) = f(2-x) - f(x)\),并证明此函数恒正,再结合 \(f(x)\) 的单调性可以推出 \(x_1+x_2>2\).
不妨设 \(x_1 < 1 < x_2\),则当 \(x_2 \geqslant 2\) 时,显然有 \(x_1 + x_2 > 2\) ,故只需考虑 \(1 < x_2 < 2\) 的情况即可.
\(x_1 + x_2 > 2\)
\(\Leftrightarrow\) \(x_2 > 2 - x_1\)
\(\Leftrightarrow\) \(f(x_2) < f(2 - x_1)\) (\(x_2, 2-x_1 \in (1, 2)\) 且 \(f(x)\) 在 \((1, 2)\) 单调递减)
\(\Leftrightarrow\) \(f(x_1) < f(2 - x_1)\) (\(f(x_1) = f(x_2)\))
故只要证 \(f(x_1) < f(2 - x_1)\) 即可,其中 \(0 < x_1 < 1\).
以上为几何对称操作,也是对称法解极值点偏移的理论基础。
下面进行求导证明 \(f(x_1)<f(2-x_1)\).
令 \(g(x) = f(x) - f(2-x)\),
则有 \(g'(x) = -\ln x(2-x)\).
有 \(0 < x < 1\) 时,\(g'(x) = -\ln x(2-x) > 0\) ,故有 \(g(x)\) 在 \((0, 1)\) 上单调递增.
又有 \(g(1) = - \ln 1 = 0\),
所以对于 \(\forall x \in (0, 1), f(x)-f(2-x)=g(x)<g(1)=0\)
也即 \(f(x)<f(2-x)\), 命题得证.
故 \(x_1+x_2>2\).
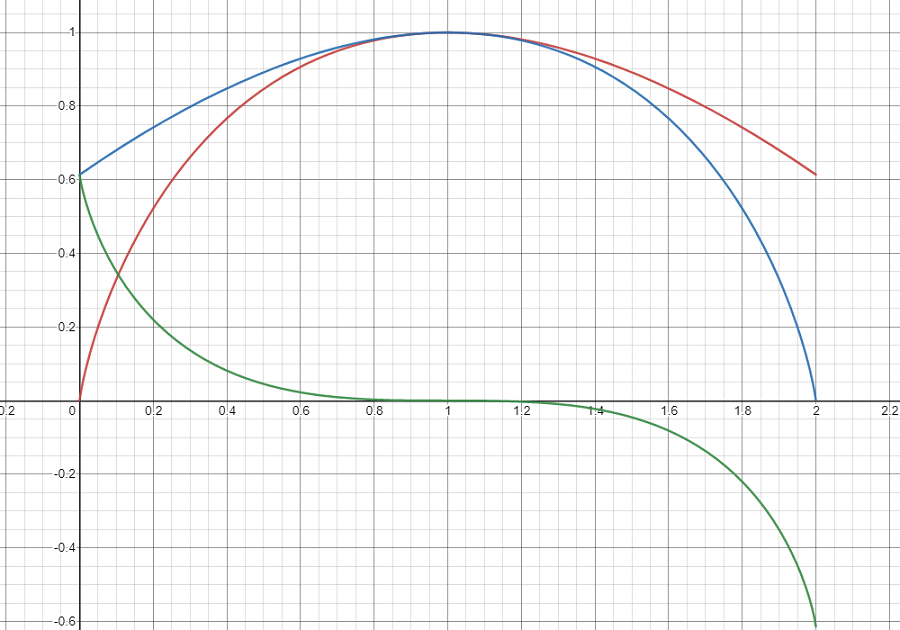
对于 \(x_1+x_2<e\) 的证明,若对称后构造函数求导,则会发现构造出的函数 \(h(x)=f(x)-f(e-x)\) 在 \((0, 1)\) 上不具有单调性,而是呈现先增后减的趋势。这样为了证明 \(h(x)>0\),我们势必要讨论 \(h(x)\) 的两个端点。但是 \(h(x)\) 在 \(x=0\) 处的端点无定义,难以讨论。
 |
 |
|---|
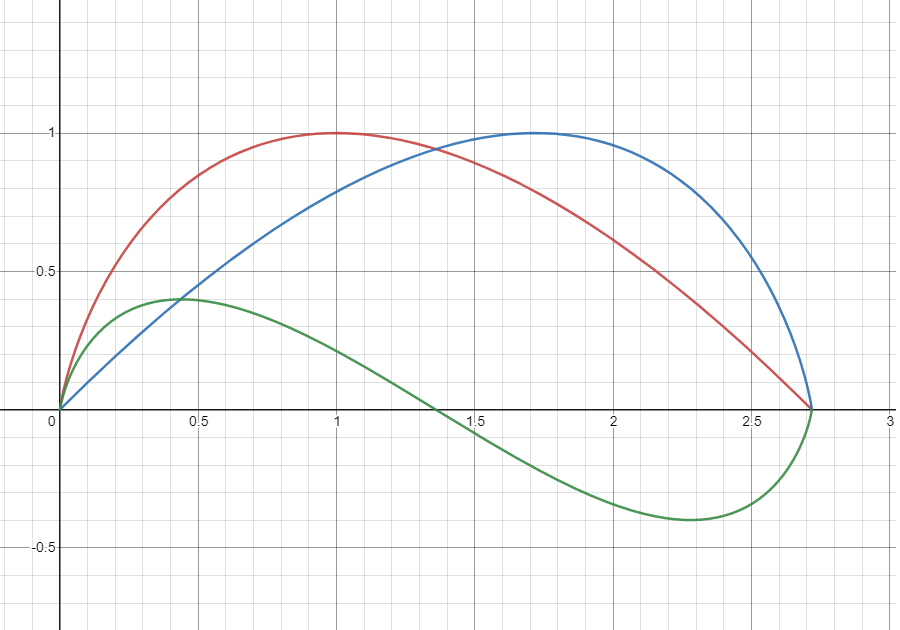
红色为原函数,蓝色为对称后的函数,绿色为相减构造出的差函数。
对于本题而言,两个方向的不等号均可以进行对称操作。对于左方向不等号而言,其构造出的函数具有单调性,可以避开 \(x\to 0\) 时的极限问题;而对于右方向不等号而言,若使用求导法解题,其构造出的函数无法避开对于 \(x\to 0\) 的极限讨论,难以证明。
再证 \(x_1+x_2<e\).
对于右方向不等号的证明,我们仍然使用对称法,在构造出函数 \(h(x)=f(x) - f(2-x)\) 后,我们使用放缩法进行不等式的证明。
仍设 \(x_1 < 1 < x_2\),则当 \(x_2 \leqslant e-1\) 时,显然有 \(x_1 + x_2 < e\) ,故只需考虑 \(e-1 < x_2 < e\) 的情况即可.
\(x_1 + x_2 <e\)
\(\Leftrightarrow\) \(x_2 < e - x_1\)
\(\Leftrightarrow\) \(f(x_2) > f(e - x_1)\) (\(x_2, e-x_1 \in (e-1, 1)\) 且 \(f(x)\) 在 \((e-1, 1)\) 单调递减)
\(\Leftrightarrow\) \(f(x_1) > f(e - x_1)\) (\(f(x_1) = f(x_2)\))
故只要证 \(f(x_1) > f(e - x_1)\) 即可,其中 \(0 < x_1 < 1\).
注意到 \(f(x)\) 在 \((e,0)\) 处导数为 \(-1\) ,故可以证明 \(f(x) < x+1\) ,将其对称过来后便可得到
\(f(e-x)<x\). 又注意到在 \((0,1)\) 区间上恒有 \(f(x)>x\) ,我们便可以以 \(y=x\) 为中介,放缩证明 \(f(e-x)<x<f(x)\). 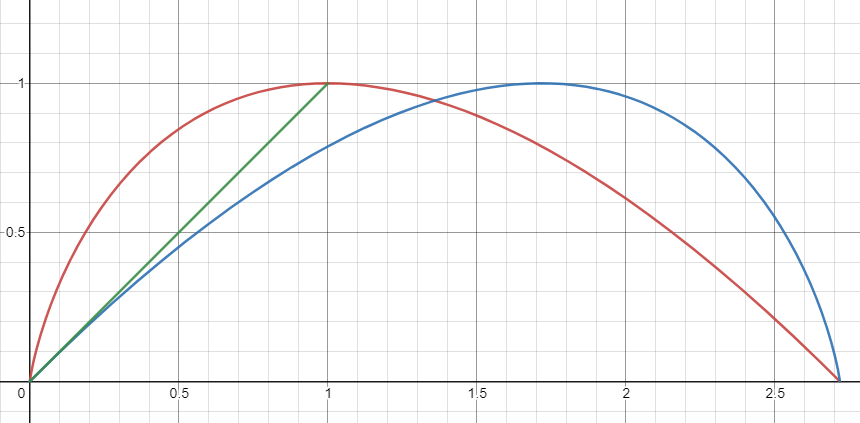
先证明 \(f(e-x)<x\).
设 \(h(x)=e-x-f(x)=e-2x+x\ln x\) ,
有 \(h'(x)=\ln x-1\).
当 \(x \in (e-1,e)\) 时,有 \(\ln x \in (\ln (e-1), 1)\) ,故有 \(h'(x)<0\) ,\(h(x)\) 在 \((e-1, e)\) 上单调减。
故有 \(h(x) > h(e) = 0\) ,即 \(e-x > f(x)\).
代入 \(e-x\) ,则有 \(f(e-x)<x\).
以上通过先证切线,后对称的方式证明了 \(f(e-x)<f(x)\).
再证明 \(f(x)>x\).
有 \(f(x)-x=-x\ln x\) ,且当 \(x \in (0, 1)\) 时, \(-x\ln x > 0\) ,故有 \(f(x)>x\).
故有 \(f(e-x)<x<f(x)\) ,又上面推导可知 \(x_1+x_2<e\).
在传统对称难有思路的时候,不妨画画图,从切线的角度思考能否用放缩解决问题。
未完待续